
NOTE参考文档见于文末
在学习数据结构的过程中遇到了一些常用的STL操作和算法知识点,下面是整理后的结果。
数组
数组支持随机访问、占用内存较少;但插入和删除元素效率低,且初始化后长度不可变特点。
基本操作
/* 初始化数组 */// 存储在栈上int arr[5];int nums[5] = { 1, 3, 2, 5, 4 };// 存储在堆上(需要手动释放空间)int* arr1 = new int[5];int* nums1 = new int[5] { 1, 3, 2, 5, 4 };增删改
/* 索引 index 处插入 num */void insert(int *nums, int size, int num, int index) { // 把索引 index 以及之后的所有元素向后移动一位 for (int i = size - 1; i > index; i--) { nums[i] = nums[i - 1]; } // 将 num 赋给 index 处的元素 nums[index] = num;}
/* 删除 index 处 */for (int i = index; i < size - 1; i++) { nums[i] = nums[i + 1];}扩容
创建->复制->释放
链表
链表通过更改引用(指针)实现高效的节点插入与删除,且可以灵活调整长度;但节点访问效率低、占用内存较多。常见的链表类型包括单向链表、环形链表、双向链表。
数组与链表的效率
| 数组 | 链表 | |
|---|---|---|
| 存储方式 | 连续内存空间 | 分散内存空间 |
| 容量扩展 | 长度不可变 | 可灵活扩展 |
| 内存效率 | 元素占用内存少、但可能浪费空间 | 元素占用内存多 |
| 访问元素 | 𝑂(1) | 𝑂(𝑛) |
| 添加元素 | 𝑂(𝑛) | 𝑂(1) |
| 删除元素 | 𝑂(𝑛) | 𝑂(1) |
增删改
/* 节点 n0 之后插入节点 P */void insert(ListNode *n0, ListNode *P) { ListNode *n1 = n0->next; P->next = n1; n0->next = P;}
/* 删除 n0 之后的首个节点 */void remove(ListNode *n0) { if (n0->next == nullptr) return; // n0 -> P -> n1 ListNode *P = n0->next; ListNode *n1 = P->next; n0->next = n1; // 释放内存 delete P;}Vector列表
列表(list)是一个抽象概念,它表示元素的有序集合,支持元素访问、修改、添加、删除和遍历等操作。列表可以基于链表或数组实现。
常用操作
//初始化vector<int> nums1;vector<int> nums = { 1, 3, 2, 5, 4 };
//末尾插入删除nums.push_back(元素);nums.pop_back();//动态数组为空时pop会出错
//中间插入删除nums.insert(nums.begin() + 3, 6); // 在索引 3 处插入 6nums.erase(nums.begin() + 3); // 删除索引 3 处
// 将列表 nums1 拼接到 nums 之后nums.insert(nums.end(), nums1.begin(), nums1.end());
//长度nums.size();
//排序sort(nums.begin(), nums.end());
//清空释放内存vector<类型>().swap(名字);一个列表类示例
class MyList { private: int *arr; // 数组(存储列表元素) int arrCapacity = 10; // 列表容量 int arrSize = 0; // 列表长度(当前元素数量) int extendRatio = 2; // 每次列表扩容的倍数
public: /* 构造方法 */ MyList() { arr = new int[arrCapacity]; }
/* 析构方法 */ ~MyList() { delete[] arr; }
/* 获取列表长度(当前元素数量)*/ int size() { return arrSize; }
/* 获取列表容量 */ int capacity() { return arrCapacity; }
/* 访问元素 */ int get(int index) { // 索引如果越界,则抛出异常,下同 if (index < 0 || index >= size()) throw out_of_range("索引越界"); return arr[index]; }
/* 更新元素 */ void set(int index, int num) { if (index < 0 || index >= size()) throw out_of_range("索引越界"); arr[index] = num; }
/* 在尾部添加元素 */ void add(int num) { // 元素数量超出容量时,触发扩容机制 if (size() == capacity()) extendCapacity(); arr[size()] = num; // 更新元素数量 arrSize++; }
/* 在中间插入元素 */ void insert(int index, int num) { if (index < 0 || index >= size()) throw out_of_range("索引越界"); // 元素数量超出容量时,触发扩容机制 if (size() == capacity()) extendCapacity(); // 将索引 index 以及之后的元素都向后移动一位 for (int j = size() - 1; j >= index; j--) { arr[j + 1] = arr[j]; } arr[index] = num; // 更新元素数量 arrSize++; }
/* 删除元素 */ int remove(int index) { if (index < 0 || index >= size()) throw out_of_range("索引越界"); int num = arr[index]; // 将索引 index 之后的元素都向前移动一位 for (int j = index; j < size() - 1; j++) { arr[j] = arr[j + 1]; } // 更新元素数量 arrSize--; // 返回被删除的元素 return num; }
/* 列表扩容 */ void extendCapacity() { // 新建一个长度为原数组 extendRatio 倍的新数组 int newCapacity = capacity() * extendRatio; int *tmp = arr; arr = new int[newCapacity]; // 将原数组中的所有元素复制到新数组 for (int i = 0; i < size(); i++) { arr[i] = tmp[i]; } // 释放内存 delete[] tmp; arrCapacity = newCapacity; }
/* 将列表转换为 Vector 用于打印 */ vector<int> toVector() { // 仅转换有效长度范围内的列表元素 vector<int> vec(size()); for (int i = 0; i < size(); i++) { vec[i] = arr[i]; } return vec; }};栈
常用操作
/* 初始化栈 */stack<int> stack;
/* 入栈 */stack.push(1);
/* 访问栈顶 */int top = stack.top();
/* 元素出栈 */stack.pop(); // 无返回值
/* 长度 */stack.size();
/* 是否为空 */stack.empty();手动实现
NOTE较为冗长,点击此处阅读
队列、双向队列
常用操作
队列
/* 初始化 */queue<int> queue;
/* 入队 */queue.push(1);
/* 访问队首 */queue.front();
/* 出队 */queue.pop();
queue.size();queue.empty();双向队列
TIP兼具栈与队列的逻辑,因此它可以实现这两者的所有应用场景,同时提供更高的自由度。
deque<int> deque;
/* 入队 */deque.push_back(2); // 添加至队尾deque.push_front(3); // 添加至队首
/* 访问 */deque.front(); // 队首元素deque.back(); // 队尾元素
/* 出队 */deque.pop_front(); // 队首元素出队deque.pop_back(); // 队尾元素出队
/* 获取双向队列的长度 */int size = deque.size();
/* 判断双向队列是否为空 */bool empty = deque.empty();实现
队列可以基于链表或者数组实现。基于链表时可以将列表的头尾节点分别视为队首和队尾,只在队尾插入只在队首删除;使用数组实现时只需要记录队首的索引、长度,通过公式计算队尾索引。
当队伍移动到数组末尾时可以使用环形数组的存储方式,对队尾索引取模可得队尾实际位置。但是实现的队列仍然具有局限性:其长度不可变。
哈希表
负载因子(load factor)是哈希表的一个重要概念,其定义为哈希表的元素数量除以桶数量,用于衡量哈希冲突的严重程度,也常作为哈希表扩容的触发条件。
哈希表的结构改良方法主要包括 “链式地址”和“开放寻址” 。
链式地址(separate chaining)将单个元素转换为链表,将键值对作为链表节点,将所有发生冲突的键值对都存储在同一链表中。当链表很长时,查询效率 𝑂(𝑛) 很差。此时可以将链表转换为“AVL 树”或“红黑树”,从而将查询操作的时间复杂度优化至 𝑂(log𝑛) 。
开放寻址(open addressing)不引入额外的数据结构,而是通过“多次探测”来处理哈希冲突,探测方式主要包括线性探测、平方探测和多次哈希等。我们不能在开放寻址哈希表中直接删除元素。
线性探测采用固定步长的线性搜索来进行探测。过哈希函数计算桶索引,若发现桶内已有元素,则从冲突位置向后线性遍历(步长通常为 1 ),直至找到空桶,将元素插入其中线性探测容易产生 “聚集现象” 。具体来说,数组中连续被占用的位置越长,这些连续位置发生哈希冲突的可能性越大,从而进一步促使该位置的聚堆生长,形成恶性循环,最终导致增删查改操作效率劣化。
平方探测与线性探测类似,都是开放寻址的常见策略之一。当发生冲突时,平方探测不是简单地跳过一个固定的步数,而是跳过“探测次数的平方”的步数,即 1,4,9,… 步。
多次哈希方法使用多个哈希函数 𝑓1(𝑥)、𝑓2(𝑥)、𝑓3(𝑥)、… 进行探测。与线性探测相比,多次哈希方法不易产生聚集,但多个哈希函数会带来额外的计算量。
常用操作
/* 初始化 */unordered_map<int, string> map;
// 添加键值对 (key, value)map[12836] = "小哈";
// 查询valuestring name = map[15937];
// 删除键值对 (key, value)map.erase(10583);
/* 遍历哈希表 */// 遍历键值对 key->valuefor (auto kv: map) { cout << kv.first << " -> " << kv.second << endl;}// 使用迭代器遍历 key->valuefor (auto iter = map.begin(); iter != map.end(); iter++) { cout << iter->first << "->" << iter->second << endl;}树
术语
- 节点所在的层(level):从顶至底递增,根节点所在层为 1 。
- 节点的度(degree):节点的子节点的数量。
- 二叉树的高度(height):从根节点到最远叶节点所经过的边的数量。
- 节点的深度(depth):从根节点到该节点所经过的边的数量。
- 节点的高度(height):从距离该节点最远的叶节点到该节点所经过的边的数量。
二叉树常用操作
插入与删除节点
TreeNode* P = new TreeNode(0);// 在 n1 -> n2 中间插入节点 Pn1->left = P;P->left = n2;// 删除节点 Pn1->left = n2;层序遍历(BFS)
可以借助队列来实现
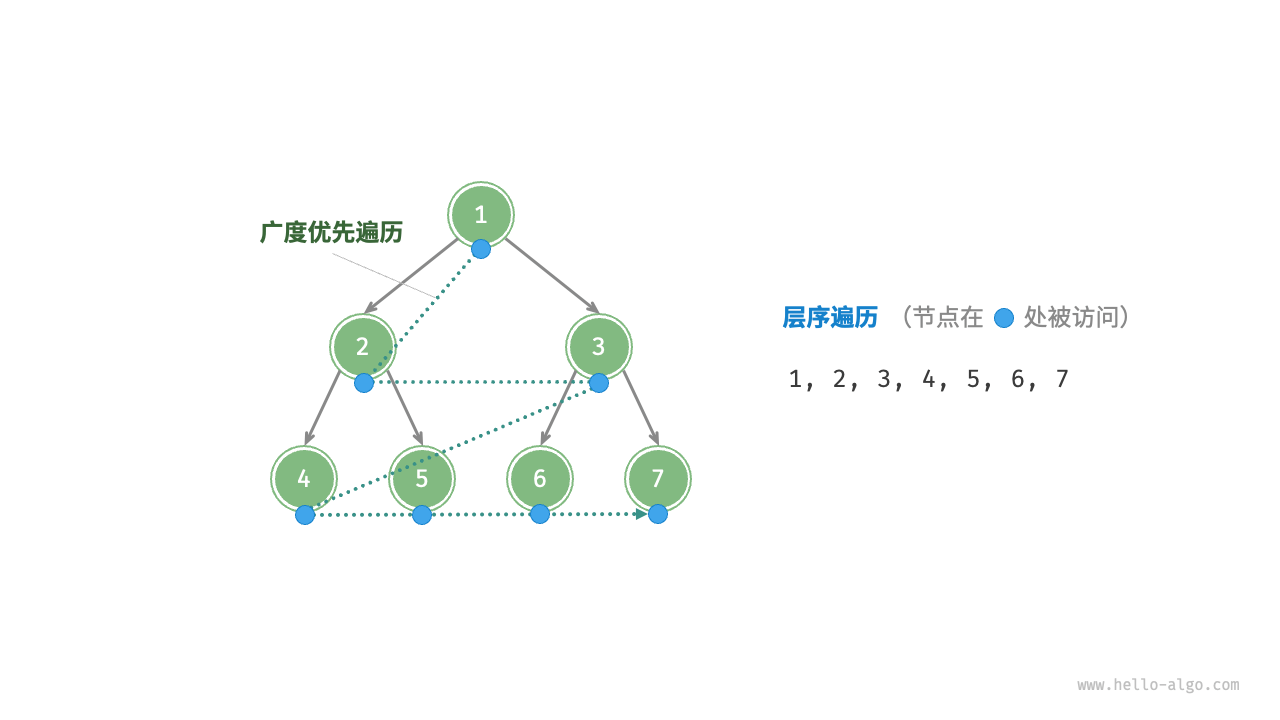
/* 层序遍历 */vector<int> levelOrder(TreeNode *root) { // 初始化队列,加入根节点 queue<TreeNode *> queue; queue.push(root); // 初始化一个列表,用于保存遍历序列 vector<int> vec; while (!queue.empty()) { TreeNode *node = queue.front(); queue.pop(); // 队列出队 vec.push_back(node->val); // 保存节点值 if (node->left != nullptr) queue.push(node->left); // 左子节点入队 if (node->right != nullptr) queue.push(node->right); // 右子节点入队 } return vec;}前中后序遍历(DFS)
深搜借助递归来实现。二叉搜索树中进行中序遍历时,总是会优先遍历下一个最小节点,从而得出一个重要性质:二叉搜索树的中序遍历序列是升序的。

/* 前序遍历 */void preOrder(TreeNode *root) { if (root == nullptr) return; // 访问优先级:根节点 -> 左子树 -> 右子树 vec.push_back(root->val); preOrder(root->left); preOrder(root->right);}
/* 中序遍历 */void inOrder(TreeNode *root) { if (root == nullptr) return; // 访问优先级:左子树 -> 根节点 -> 右子树 inOrder(root->left); vec.push_back(root->val); inOrder(root->right);}
/* 后序遍历 */void postOrder(TreeNode *root) { if (root == nullptr) return; // 访问优先级:左子树 -> 右子树 -> 根节点 postOrder(root->left); postOrder(root->right); vec.push_back(root->val);}实现
完全二叉树可以用数组来实现,但是不适合存储数据量过大的树,增删节点需要通过数组插入与删除操作实现,效率较低。
/* 二叉搜索树查找 */TreeNode *search(int num) { TreeNode *cur = root; while (cur != nullptr) { // 目标节点在 cur 的右子树中 if (cur->val < num) cur = cur->right; // 目标节点在 cur 的左子树中 else if (cur->val > num) cur = cur->left; else break; } // 返回目标节点 return cur;}AVL树、B树、红黑树
AVL树(Adelson-Velsky and Landis树)是一种自平衡的二叉搜索树。它通过在每个节点上维护平衡因子(即左子树和右子树的高度差)来确保树的平衡,从而保证基本操作的时间复杂度为O(log n)。每次插入或删除操作后,AVL树会通过旋转操作来重新平衡树。
与二叉搜索树不同,B树的节点可以有多个子节点。适用于大规模数据存储,因为它可以高效地进行范围查询和顺序遍历,并且由于其节点可以存储多个键值对,它减少了需要访问磁盘的次数,从而提高了性能。
红黑树(Red-Black Tree)是一种自平衡的二叉搜索树。它通过在每个节点上附加一个颜色属性(红色或黑色)来保持平衡,确保树的高度大致为O(log n)
实现细节可以参考CS61B的七海版教学:七海讲数据结构,质量很好也很有趣。

堆
需要指出的是,许多编程语言提供的是优先队列(priority queue),这是一种抽象的数据结构,定义为具有优先级排序的队列。
实际上,堆通常用于实现优先队列,大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看,我们可以将“优先队列”和“堆”看作等价的数据结构。
常用操作
/* 初始化堆 */// 初始化小顶堆priority_queue<int, vector<int>, greater<int>> minHeap;// 初始化大顶堆priority_queue<int, vector<int>, less<int>> maxHeap;
/* 元素入堆 */maxHeap.push(1);
/* 获取堆顶元素 */maxHeap.top();
/* 堆顶元素出堆 */// 出堆元素会形成一个从大到小的序列maxHeap.pop(); //c++中无返回值,python有
maxHeap.size();maxHeap.empty();
/* 输入列表并建堆 */vector<int> input{1, 3, 2, 5, 4};priority_queue<int, vector<int>, greater<int>> minHeap(input.begin(), input.end());实现
完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树,因此可以采用数组来存储堆。
节点指针通过索引映射公式来实现。给定索引 𝑖 ,其左子节点的索引为 2𝑖+1 ,右子节点的索引为 2𝑖+2 ,父节点的索引为 (𝑖−1)/2(向下整除)。当索引越界时,表示空节点或节点不存在。

添加元素之后,由于 值 可能大于堆中其他元素,堆的成立条件可能已被破坏,因此需要修复从插入节点到根节点的路径上的各个节点,这个操作被称为堆化(heapify)。从入堆节点开始,从底至顶执行堆化。出堆时根节点开始,从顶至底执行堆化
参考资料
- 你好,算法!Github
- Krahets 笔面试精选 88 题 LeetCode
- 图解算法数据结构 LeetCode
- 大话数据结构 Douban
